3種類以上のデータの有意差検定はエクセル関数では対応していません。無料でこれを行う手段として統計解析ソフトRがありますが、慣れて活用できるまで時間がかかります。
本サイトではテンプレに必要事項を入力してRにコピペすることで簡単に有意差検定を行うツールを提供します。
サポートしているエクセルデータの形式は以下のようなものです。
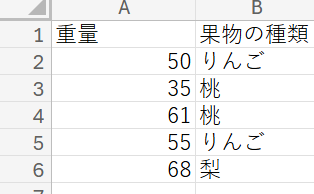
カテゴリーごとの数値の平均値に有意差があるかを判定します。以下のデータでは果物の種類ごとの重量の平均値の有意差を判定します。
今後、グラフ描図に関しても対応予定です。
1 Excelファイルの読み込み
・作業ディレクトリの変更
こちら(別タブで開きます)を参考にして、現在のディレクトリを使用するエクセルファイルが存在するフォルダに変更します。
・読み込むエクセルシートの指定方法の選択
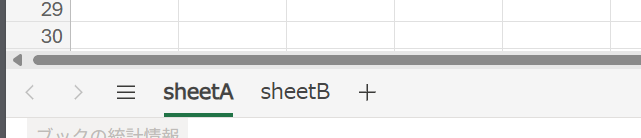
上のエクセルファイルを例に説明します。デフォルトでは一番目のシート、sheetAが読み込まれます。
2番目以降のシートを読み込む場合、シート指定方法を変更する必要があります。
sheetBを読み込む場合、シート名を指定する方法ではsheetBをsheetの名前の空欄に入力します。シート番号を指定する場合、sheet番号の空欄に何番目のシートかを入力します。sheetBは2番目のシートのため2と入力します。
・エクセル情報の入力とコピペ
以下の空欄にエクセルファイル名などを入力した後、copyボタンを押して、コードをコピーします。Rの>の後にペーストしてEnterを押して実行します。
install.packages("openxlsx", repos = "cloud.r-project.org");
library(openxlsx);
data = read.xlsx(".xlsx")
library(openxlsx);
data = read.xlsx(".xlsx")
Copy
2 Excelデータのヘッダーの入力
下の空欄に入力後setボタンを押します。この手順以降のテンプレに入力値が反映されます。データのヘッダー名の空欄には数値データのエクセルファイル上のヘッダー名(写真の例では「重量」)を入力。グループのヘッダー名には数値データのカテゴリー名(写真では「果物の種類」)を入力します。

データのヘッダー名 グループのヘッダー名
Set
3 等分散検定(Bartlett test)
データに応じてより正しい結果を得るために、有意差検定の方法を選びます。この手順3と次の4の結果をもとに5の有意差検定の方法を決めます。2でヘッダー名、グループ名がセットされているなら、Rに1と同様にコピペしてください。
bartlett.test(data$"" ~ data$"")
Copy
下はRの結果の例です。このp-valueが0.05より大きければデータは等分散です。
Bartlett test of homogeneity of variances
data: data$e068 by data$shoriku
Bartlett's K-squared = 10.579, df = 3, p-value = 0.014244 正規性検定
3と同様にRで実行してください。同様にp-valueが0.05より大きければデータは正規分布しています。
install.packages("onewaytest", repos = "cloud.r-project.org");
library(onewaytest);
nor.test( ~ , data = data)
library(onewaytest);
nor.test( ~ , data = data)
Copy
5 有意差検定
3と4によりデータが等分散かどうかそして、正規分布かどうかわかりました。これをもとに検定方法を選択しRで実行してください。
・検定方法の選択
summary(aov(data$ ~ data$
, data = data))
Copy
Krasukal wallis test
kruskal.test(data$"",data$"")
Copy
Wilcox test
pairwise.wilcox.test(data$, data$, p.adj = "bonf")
Copy
Brunner Munzel test
install.packages("lawstat", repos = "cloud.r-project.org");
library(lawstat);
brunner.munzel.test(data$, data$)
library(lawstat);
brunner.munzel.test(data$, data$)
Copy
diff lwr upr p adj
りんご-桃 -0.01373369 -0.3023816 0.2749142 0.9911629
もも-梨 0.50300842 0.2143605 0.7916564 0.0015031
梨 -りんご 0.51674212 0.2280942 0.8053901 0.0012126上記のような結果が得られるはずです。このp adjの値が0.05より小さければ有意差ありと判定します。上記では桃となし、そして梨とりんごの重量にはそれぞれ有意差がありませんが、りんごと桃の重量に有意差はあります。

コメント